Contribution à la problématique du choix des paysages de |
recherche locale stochastique : |
Le cas des règles de Golomb. |
Pour l'obtention du Diplôme d'Etudes Approfondies En Informatique, Automatique et Productique
La recherche locale constitue une arme redoutable pour attaquer des problèmes de grande taille réputés très difficiles tels que le
voyageur de commerce et la partition de graphes.
La recherche locale représente un outil puissant pour résoudre les problèmes réputés difficiles
(notamment NP-complet) tels que la coloration de graphes, le problème du sac à dos, le problème du voyageur de commerce.
Mais la conception d'un algorithme de recherche locale dédié à un problème nécessite de faire des choix concernant la
stratégie de recherche (c'est à dire la manière dont notre problème va être résolu), l'espace de recherche, le voisinage,
la fonction objectif, les paramètres de contrôle de la recherche.De manière générale les concepteurs font ces choix de manière
empirique ou en ce basant sur des travaux expérimentaux antérieurs.
La recherche locale se base sur deux éléments fondamentaux, la stratégie de recherche ainsi que
l'espace de recherche. Notre objectif est de proposer une méthode de choix d'un paysage de recherche basé
sur l'étude expérimentale de plusieurs variantes de paysages avec un même algorithme de référence : Métropolis.
Le cadre expérimental que j'ai choisi pour illustrer cette approche est celui de la recherche de règles de Golomb.
Ce problème a été choisi parce qu'il est difficile (on ne sait le résoudre qu'en temps exponentiel) et qu'il nous
permet de décliner plusieurs variantes de paysages de recherche basés sur des voisinages différents.
D'autre part, il y a peu de publications scientifiques qui abordent la recherche des règles de Golomb par des méthodes de recherche
locale stochastique. De ce fait il nous parait intéressant de vérifier la traitabilité de ce problème avec cette approche.
L'algorithme implémenté (Métropolis) est contrôlé par un paramètre appelé température. Pour chaque variante de paysage, nous déterminons
la valeur optimale de la température sur la basede statistiques d'exécutions, puis nous étudions
l'évolution de cette valeur en fonction de la taille des règles de Golomb recherchées.
La validité de notre approche repose sur l'hypothèse que le paysage de recherche (parmi ceux étudiés) qui donne le meilleur résultat avec
Métropolis est également le paysage le plus performant avec des stratégies de recherche plus élaborées.
Le rapport est organisé comme suit : la première partie représente un état de l'art qui contient deux chapitres, nous présentons en
chapitre 1 quelques notions sur la recherche locale et quelques variantes comme le recuit simulé.
En chapitre 2 nous présentons le problème de la recherche des règles de golomb qui servirent de base à nos expérimentations.
Dans la deuxième partie (chapitre 3) nous introduisons deux paysages associés au problème de recherche de règles de Golomb,
puis nous présentons une étude empirique de l'efficacité de Métropolis sur ces deux paysages. Nous développons
l'idée d'utiliser une telle démarche comme base d'une méthode de choix d'un paysage de recherche lors de
la conception d'un système de recherche locale stochastique.
La recherche locale , appelée aussi " descente " ou " amélioration itérative ",
représente une classe d'heuristiques très anciennes. Traditionnellement, la recherche locale constitue une
arme redoutable pour attaquer des problèmes réputés très difficiles tels que le voyageur de commerce et la partition de graphes.
Une méthode de recherche locale est un processus itératif fondé sur deux éléments essentiels :
la notion de paysage de recherche et celle de stratégie de recherche.
Le paysage de recherche on peut le représenter sous la forme d'un graphe dont les sommets sont associés
aux configurations de l'espace de recherche et dont les arrêtes définissent une relation de voisinage.
A chaque configuration est associée une valeur d'objectif qui peut être un entier dont la valeur est minimale pour les solutions.
La stratégie de recherche c'est elle qui détermine la manière dont le paysage de recherche sera exploré.
Les règles ordinaires ont leurs marques également espacées par une certaine unité de mesure (par exemple 1 centimètre), ainsi quelqu'un peut mesurer n'importe quelle distance entre 1 et la longueur de la règle en plaçant un segment entre deux marques quelconques de la règle. Par exemple pour mesurer une distance de 5 centimètres, il est possible de placer un segment entre les marques de 0 et 5 ou 1 et 6 centimètres etc.
 Règle Ordinaire |
|
 Règle de Golomb |
Les règles de Golomb peuvent être considérées comme un genre spécial de règles. Pour qu'une règle soit une règle de Golomb, elle doit
avoir seulement un seul choix au plus si on veut mesurer une distance spécifique. Plus précisément chaque distance entre
deux nombres (de marques) doit être différente de tous les autres.
Par exemple s'il y a une marque à la position 2 et une autre a la position 5, aucune autre paire des marques doit être séparée
par une distance de 3. De cette définition il découle qu'une règle ordinaire avec plus de 2 marques n'est pas une règle de Golomb.
La règle de Golomb de la figure 3 peut mesurer les distances {1, 2, 3, 4, 5, 7, 8, 9, 10, 11} avec un choix approprié,
des marques ; et aucune autre distance ne peut être mesurée. Pour chacune de ces distances, seulement une paire de
marques peut être employée pour faire une telle mesure, donc la propriété de Golomb est satisfaite.

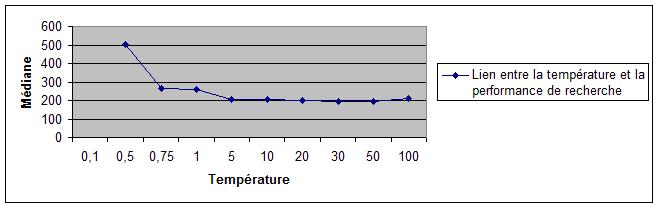
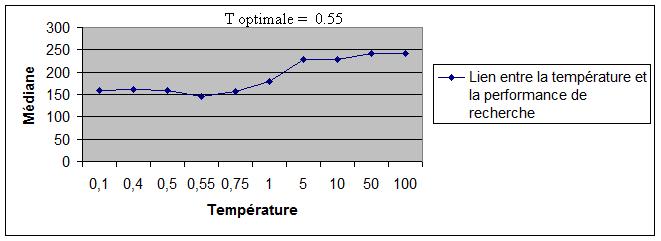
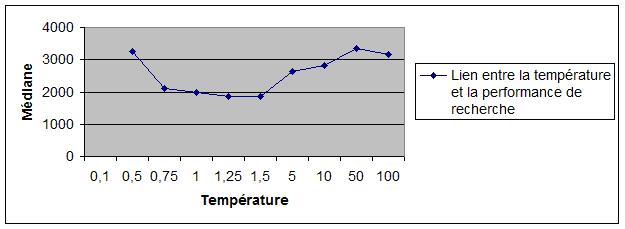
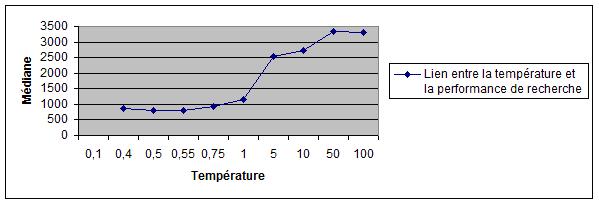
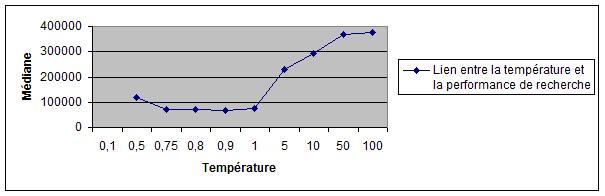
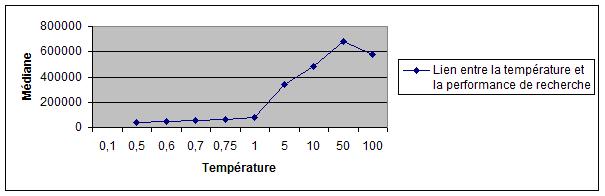
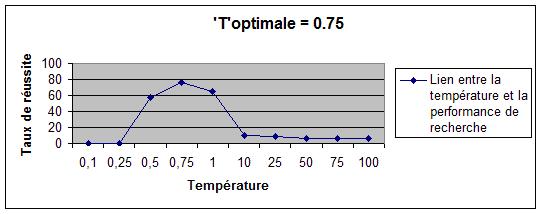
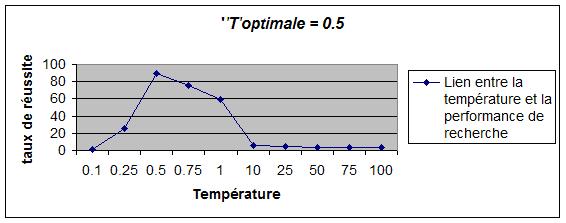
| Mediane V2 / Mediane V1 | 0.7474 | 0.4268 | 0.5961 | 0.5978 |
| Règles | K = 6 / L = 17 | K = 7 / L = 25 | K=8 / L = 34 | K = 9 / L = 44 |
Nous avons mis en évidence l'impact du choix du voisinage sur l'efficacité d'une résolution d'un problème combinatoire la recherche des règles de Golombs, en fixant le processus étudié (Métropolis) et en variant les paysages. Nous avons proposé une méthode de comparaison et de choix de paysages de recherche basée sur l'évaluation des paysages candidat à l'aide de Métropolis, pour comparer l'efficacité des relations de voisinages.
L'approche proposée peut également être utilisée pour :
Mais ceci ne constitue qu'un premier défrichage car beaucoup de questions restent ouvertes :
Quelles sont les limites de la robustesse de la méthode vis avis d'un plus large panel de stratègies de recherche (si un paysage est meilleur qu'un autre pour une stratégie de recherche , le demeure t-il pour toutes les stratégies de recherche ?) et de problèmes (la méthode est elle généralisable à n'importe quel problème).
Peut on améliorer le choix de voisinage en utilisant d'autres critères tels que par exemple des mesures de correlation voisinage-coût.